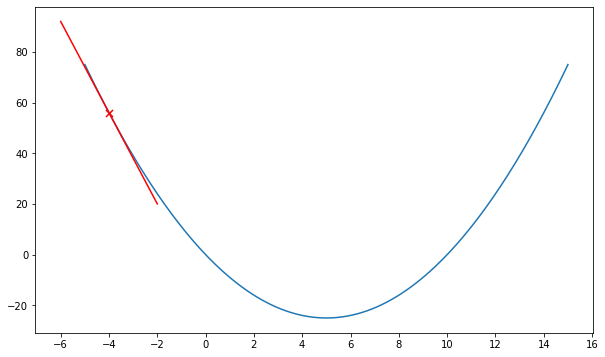
Gradient descent is an optimization algorithm for finding a local minimum of a differentiable function. The algorithm iteratively updates the parameters of the function by computing the gradient of the function. Consider a differentiable function, ![]() as shown in Figure 1. We know that the function is minimum when
as shown in Figure 1. We know that the function is minimum when ![]() . Assuming that
. Assuming that ![]() , to get to the minimum, we need to move to the “left”. Specifically, we need to update
, to get to the minimum, we need to move to the “left”. Specifically, we need to update ![]() by subtracting a value from it. To determine the value that we need to subtract from
by subtracting a value from it. To determine the value that we need to subtract from ![]() , we compute the gradient at
, we compute the gradient at ![]() which is the slope of the tangent line at the given point. In other words, the gradient is the rate of change of the function at a given point.
which is the slope of the tangent line at the given point. In other words, the gradient is the rate of change of the function at a given point.
Given a function, the gradient is computed by taking the derivative of the function with respect to its parameter.
![]()
Then, the parameter is updated iteratively until optimal solution is obtained as follows:
Repeat until converge: ![]()
where ![]() is the step size or learning rate.
is the step size or learning rate. ![]() controls the amount of the update to be applied to the parameter
controls the amount of the update to be applied to the parameter ![]() . A small
. A small ![]() corresponds to a little step which means the optimization will take longer to complete while a large
corresponds to a little step which means the optimization will take longer to complete while a large ![]() may cause the gradient descent to overshoot (miss the minimum) and fail to converge.
may cause the gradient descent to overshoot (miss the minimum) and fail to converge.
Let’s analyze the parameter update equation. Consider ![]() as shown in Figure 1. For now, assuming
as shown in Figure 1. For now, assuming ![]() . We know that
. We know that ![]() (positive value). Based on the update equation,
(positive value). Based on the update equation, ![]() will be reduced by the value of
will be reduced by the value of ![]() .
.
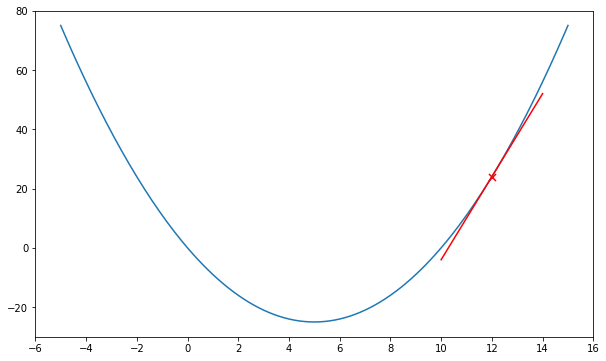
If ![]() is to the left of the minimum as shown in Figure 2. We know
is to the left of the minimum as shown in Figure 2. We know ![]() (negative value). Based on the update equation,
(negative value). Based on the update equation, ![]() will be increased by the value of
will be increased by the value of ![]() .
.